Floral Automata

Scott Aaaronson has long been one of my greatest contemporary idols in computer science and physics. I became acquainted with his writing through “Who Can Name the Bigger Number”, which is perhaps the most exciting and accessible introduction to theoretical computer science for a lay audience. Also his is the excellent survey on the feasibility of NP-Complete computation by physical means (”NP-Complete Problems and Physical Reality”) and the summary of quantum computing “Quantum Computing Since Democritus”. But undoubtedly my favorite piece of writing by Aaronson is “Why Philosophers Should Care About Computational Complexity”, in which he argues (among other things) that we should reframe philosophical questions in the language of computational complexity theory.

The marriage between philosophy and complexity leads us to Sean Carroll, which is a superb scientist in his own right (Sean is a physicist at Caltech). Carroll has long been interested in the evolution of complexity in the universe. Entropy always increases, of course, but complexity is something else entirely: while the entropy of a closed system grows monotonically, the apparent complexity of the same system initially increases but ultimately subsides. The metaphor of choice is the mixing of coffee and cream in a cup: a system initially simple to describe (a two-layer, heterogeneous mixture) which gradually becomes complicated with intricate spirals and fractal arms until it experiences its own petite “heat death” and becomes once again simple to describe as a homogeneous brown mixture. Carroll’s point is that the coffee-cream metaphor matches what we see in our universe. The singularity at the beginning of time is low-entropy, then statistical mechanics comes into play and entropy increases along with complexity (atoms, then molecules, planets, planetary systems, galaxies, life itself). But eventually our universe will reach thermal equilibrium at which point all complex structures will be long gone.

Coffee and cream mixing.

Aaronson and Carroll wrote a paper together with the goal of framing this subjective notion of complexity into a rigorous context. Here is their insight: when coffee and cream are mixed together, we perceive their complexity in macroscopic terms. Ultimately you have an ever more random configuration of coffee and cream particles, but macroscopically if you gaze at an homogeneous mixture you won’t perceive it as complex — you’ll just perceive it as another shade of gray (brown in this case). The bottom line is that “mostly coffee” areas should be perceived as black, “mostly cream” areas should be perceived as white and really random areas should be perceived as gray. Aaronson and Carroll formalize this by defining a bidimensional “coffee automaton” which is initialized with 50% black particles at the bottom and 50% white particles at the top. There is a simple stochastic rule determining the mixing process: randomly two neighbor particles will exchange places. A simulation is then run with these rules and screenshots are taken as it evolves. Each screenshot is compressed with a lossless file compressor such as gzip. The size of the compressed file should give an approximation of the entropy of the system (how much irreducible information is there). This entropy evolves as we would expect, logarithmically. But the interesting part is their formalization of complexity. What they do is they take the same screenshot, blur it and apply a 3-level thresholding. Mixed areas become gray, black areas remain black and white areas remain white. The image is then compressed and the resulting file size is a measure of macroscopic complexity. As our perception from the coffee and cream metaphor suggests, this complexity initially increases but ultimately subsides.

I think Aaronson and Carroll’s idea has a huge potential for generative art. But before I get into that, let’s briefly define a cellular automaton. A cellular automaton, in its crudest form, is a row of black-or-white cells coupled with an update rule. The update rule tells each cell how to update its color (to black or white) given the color of its two neighbors and its own. When you draw the evolution of the configurations of this row of cells through time interesting patterns emerge, such as in the example above (time runs in the top-down direction) which reproduces a Sierpinski triangle.

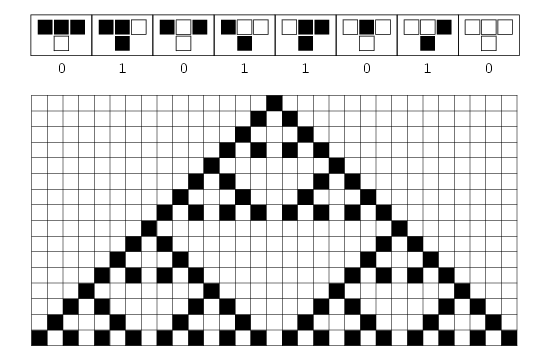“Rule 90” elementary cellular automaton.

When you implement a cellular automaton, you may either choose to make the leftmost and rightmost cells have a single neighbor or to make them neighbors of each other, therefore embedding the row of cells into a circular topology. The best way to visualize this is by arranging cells in a circle, such as in the image below.

Of course this is just one of many such automata (256 to be exact). They come in very different shapes (see for example rules 18, 30, 57, 60, 89 in the album below):

Some of these rules however yield unpleasant “mandalas” as they exhibit high contrast regions. This is the case of Rule 30, for example. Aaronson and Carroll’s technique then comes in handy: what if we blur these mandalas and apply 3-level thresholding? Well, we get some very interesting images:

By applying the macroscopic perspective on these automata, we can distinguish between chaotic and orderly regions and thus unmask their apparent complexity. Plus we get rid of the pixelated look, replacing it for an organic, smooth feel. But better yet: what happens if we apply blurring + thresholding in real-time?

We can also increase the number of cell colors (from the binary black-and-white setup), yielding something like this:

To deal with the considerable number of parameters involved in producing these images, I implemented a little interactive tool in Processing. It allows you to choose the tape (row) size, expand the neighborhood size beyond your immediate neighbors, increase the number of symbols/colors and also to calibrate the blur intensity and choose the K in the K-level thresholding treatment. The project is available on GitHub.

GUI of the floral automata interactive tool implemented in Processing

This little experiment was personally very satisfying to me because I think it ties together a number of features which render a generative art project successful. First, the state space of possible outputs should contain a decent density of interesting results. This is certainly the case with elementary cellular automata, which exhibit a colorful zoo of patterns in just 256 rules. Second, symmetry is very appealing. In this experiment we were able to enforce symmetry by running automata on a circular topology and by initializing the tape with 8 equally spaced black cells — this enforces 8-fold symmetry. Third, although symmetry is important, it is also good to have a little chaos. In fact, I believe the fine balance between order and chaos is paramount to the beauty of artwork in general an generative art in particular. In this case we lend our success to the inherent complexity of some cellular automaton rules and crucially to the blurring + thresholding treatment which allows us to perceive chaos more aesthetically.